
5990
.pdf
Стоит помнить, что матрица жесткости симметрична и поэтому |
|
|||
K |
|
= K |
T . |
(7.23) |
|
ij |
|
ij |
|
Наполнение векторов { i} и {Fi}, относящихся к отдельной узловой точке,
зависит от характера решаемой задачи.
Так, при решении задачи определения напряженного состояния тонкой пластины, нагруженной в своей плоскости (плоская задача теории упругости),
указанные векторы могут иметь следующую структуру: |
|
|||||
{ |
|
}= |
ui |
, |
|
(7.24) |
|
i |
|
|
|
|
|
|
|
|
vi |
|
|
|
{ |
|
}= |
Pxi |
|
, |
(7.25) |
Fi |
|
|
|
|
|
|
|
|
|
Py i |
|
|
|
где ui ,vi - смещения i-го узла по осям x и y, а компоненты |
Pxi и Py i - узловые силы, |
|||||
приложенные в этом узле (рис 7.2). |
|
|
|
|
|
|
Pyi , vi
Pxi , ui
Рис. 7.2
При решении задачи изгиба пластины наполнение указанных векторов будет совсем другим:
|
wi |
|
|
{ |
|
|
|
i} = θxi |
|
(7.26) |
|
|
|
|
|
|
θyi |
, |
|
|
Pi |
|
|
|
|
|
|
{Fi} = M xi |
(7.27) |
||
|
|
|
, |
|
M yi |
||
60
где Pi - узловая сила, приложенная по нормали к поверхности плиты (вдоль оси z);
Mxi , M yi - пары сил, приложенных в i-м узле соответственно в плоскостях xz и yz;
wi , θxi , θyi - прогиб и угловые перемещения (повороты) i-го узла в тех же
направлениях.
Имея величины перемещений в узлах, перемещения во внутренних точках элемента можно выразить путем интерполяции с помощью набора алгебраических функций Ni , которые известны как функции формы. Это делается с помощью формулы
7.5 следующим образом: |
|
|
|
|
|
|
|
|
|
{ |
1} |
|
|
|
|
|
|
|
n |
|
{u}= [N]{ Э}= [[N1] |
[N2] ... |
[Nn]] |
{ |
2} |
= ∑[Ni]{ i}, |
|
|
|
(7.28) |
||||
|
|
|
... |
i=1 |
|
|
|
|
|
{ |
n} |
|
|
где n – число узловых точек конечного элемента, |
причем блоки [N i] |
имеют |
||||
диагональную структуру и могут быть построены по правилу: |
|
|
||||
[N i]= N i [I ], |
|
|
|
|
(7.29) |
|
где [I ] - единичная матрица размером m × m , а m - число степеней свободы в узле. |
||||||
В качестве примера приведем структуру матрицы функций формы для |
||||||
трехузлового конечного элемента с двумя степенями свободы в узле: |
|
|||||
N1 0 |
N2 0 |
N3 |
0 |
|
(7.30) |
|
[N]= |
|
|
|
|
|
|
0 N1 |
0 N2 |
0 N |
3 . |
|
|
|
Матрица деформаций [B] в соответствии с формулой (7.9) формируется путем умножения матричного оператора [L] на матрицу функций формы [N ]. По этой причине матрица [B], как и матрица функций формы [N], будет иметь блочную структуру:
[B]= [L][N ]= [L][[N1] [N 2] ... [N n]] = [[B1] [B2] ... [Bn]]. (7.31)
Тогда соотношение (7.8) для элемента, содержащего n узлов, может быть развернуто следующим образом:
|
|
|
{ |
1} |
|
|
|
{ε} = [B]{ |
el}= [B1] [B2] |
... [Bn] |
{ |
2} |
n |
|
|
|
|
= ∑[Bi]{ i}. |
(7.32) |
||||
|
|
|
|
... |
i=1 |
|
|
|
|
|
{ |
n} |
|
|
|
|
|
|
|
|
|
|
|
61

7.3.Сборка глобальной системы уравнений МКЭ
Для разъяснения процедуры сборки глобальной матрицы жесткости и глобального вектора узловых сил рассмотрим для начала простой пример стержня, загруженного осевой нагрузкой представленного двумя квадратичными конечными элементами типа 1D3 (рис.7.3). Каждый i-й узел такого конечного элемента будет иметь одну степень свободы.
Рис. 7.3 Предположим, что для каждого из двух элементов вычислена матрица жесткости
и вектор узловых сил. Таким образом, мы имеем в распоряжении следующие матрицы:
|
|
|
k11 |
k12 |
k13 |
|
|||||||||||
K I |
= |
k22 |
|
|
|
|
|
||||||||||
|
|
|
k21 |
k23 |
|
||||||||||||
|
|
|
|
k32 |
|
|
|
|
, |
||||||||
|
|
|
k31 |
k33 |
|
||||||||||||
|
|
|
|
|
|
33 |
|
|
34 |
|
|
|
35 |
|
|
||
|
|
|
k |
|
k |
|
|
k |
|
||||||||
KII |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
k 44 |
k 45 |
|
|||||||||||||
|
|
|
k 43 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||
|
|
|
|
k 54 |
k 55 |
||||||||||||
|
|
|
k 53 |
|
|
||||||||||||
|
|
|
f |
1 |
|
|
|
||||||
{F |
I |
|
|
|
|
|
|||||||
|
}= f |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
, |
|
|||||
|
|
|
f |
3 |
|
(7.33) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
f |
3 |
|
|
|||||||
{F |
II |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||
|
}= f |
4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
f 5 |
. |
|
|
|||||||
Потенциальная энергия каждого КЭ может быть вычислена следующим
образом:
ΠI = 12 {uI}T [K I ]{uI} −{uI}T {F I} =
= |
1 |
(u1(k11u1 + k |
12u2 + k13u3)+ u2 (k |
21u1 + k22u2 + k23u3)+ |
(7.34) |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+u3 (k31u1 + k32u2 + k33u3))− ( f 1u1 + f 2u2 + f 3u3). |
|
|
|
||||||||||||||||||||||||||||||||||||
ΠII = |
1 |
{uII}T [K II ]{uII} −{uII}T {F II} = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
1 |
(u3 ( |
|
|
|
u3 + |
|
|
|
u4 + |
|
|
u5)+ u4 ( |
|
|
u3 + |
|
|
|
u4 + |
|
u5)+ |
(7.35) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
k 33 |
|
|
k 34 |
|
|
|
|
k 35 |
k 43 |
|
|
k 44 |
|
|
|
k |
45 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
+u5 ( |
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
u5))− ( |
|
u |
3 + |
|
|
|
4 + |
|
|
u5). |
|
|
||||||||||
|
|
|
|
|
u3 |
|
|
|
u4 |
|
|
|
|
f |
f |
|
u |
f |
|
|
|
||||||||||||||||||
|
|
|
|
|
k 54 |
k 55 |
4 |
5 |
|
|
|||||||||||||||||||||||||||||
|
|
|
k 53 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
62

Общая потенциальная энергия равняется сумме потенциальных энергий
элементов (7.34) и (7.35): |
|
Π = Π I + Π II . |
(7.36) |
Теперь применим теорему о минимуме потенциальной энергии системы. Приравнивая к нулю первые производные от потенциальной энергии (7.36) по
каждому из узловых перемещений, получим:
∂Π
∂u1∂Π∂u2
∂Π
∂u3∂Π
∂u4
∂Π
∂u5
=k11 u1 + k12 u2 + k13 u3 − f 1 = 0
=k21 u1 + k22 u2 + k23 u3 − f 2 = 0
(7.37)
= k31 u1 + k32 u2 + (k33 + k 33) u3 + k 34 u1 + k 35 u2 −( f 3 + f 3) = 0
=k 43 u3 + k 44 u4 + k 45 u5 − f 4 = 0
=k 51 u3 + k 52 u4 + k 53 u5 − f 5 = 0.
Сформированная система уравнений (7.37) может быть записана в матричной
форме:
k11 |
k12 |
k13 |
0 |
|
0 |
u1 |
|
|
|
|
f 1 |
|
|
|
||||||||||||||
k21 |
k22 |
k23 |
0 |
0 |
|
u2 |
|
|
|
|
f 2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k31 |
k32 |
(k33 + k 33) |
k 34 |
k 35 |
|
u3 |
|
= |
f |
3 + f |
3 |
|
(7.38) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u4 |
|
|
|
|
|
|
|
|
|
||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
4 |
|
|
||||||||
k |
43 |
k 44 |
k 45 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
. |
|
k 53 |
k 54 |
|
|
|
|
|
5 |
|
|
|
||||||||||||||||||
|
|
|
k 55 |
u5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Видно, что коэффициенты жесткости в формуле 7.38, относящиеся к 3-му узлу и входящие в матрицы жесткости, как первого, так и второго элементов, при сборке матрицы жесткости всей конструкции суммируются.
Несколько более сложный характер будет иметь процесс сборки для двумерных и трехмерных сеток конечных элементов. Продемонстрируем порядок формирования глобальных матриц на примере плоской сетки состоящей их трех квадратичных конечных элементов типа 2D8 (рис. 7.4). На приведенном рисунке показана общая (глобальная) нумерация узловых точек сетки.
63
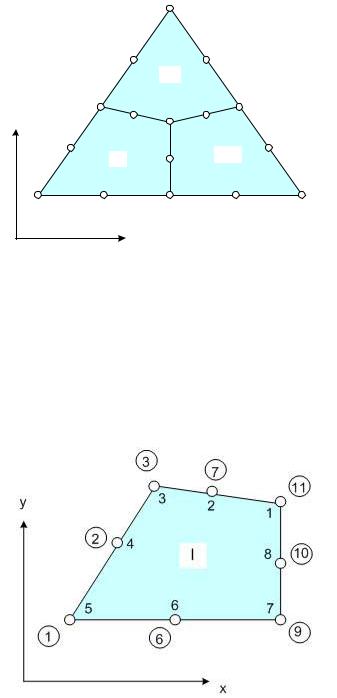
Рис. 7.4 Для начала рассмотрим первый конечный элемент (рис. 7.5). В кружочках
приведены глобальные номера узлов сетки, а внутри конечного элемента указана против часовой стрелки их локальная нумерация от 1 до 8, начиная с правого верхнего узла.
Рис. 7.5 Матрица жесткости данного элемента может быть представлена в блочном виде
(рис. 7. 6), на котором каждый квадратный блок |
K |
имеет размерность m×m, где m- |
|
|
ij |
число степеней свободы в узле, и содержит, |
как указывалось выше, реакции, |
|
возникающие в i-м закрепленном в результате |
смещений j-й узловой точки. Блоки |
|
матрицы жесткости элемента упорядочены в соответствии с локальной нумерацией узлов, но указаны также и их глобальные номера. Поскольку матрица жесткости
64

обладает свойством симметрии, отсутствует необходимость в хранении ее нижней треугольной части. На рис. 7.6 показан и вектор узловых сил данного конечного элемента.
При включении коэффициентов жесткости и узловых сил, относящихся к данному конечному элементу, в соответствующие глобальные матрицы, необходимо учитывать несоответствие глобальной и локальной нумерации узлов элемента. Так, например, блок [K3,4] в глобальной матрице жесткости (рис. 7.7) должен стоять на пересечении 3-й строки и 2-го столбца и, в силу симметрии, на пересечении 2-й строки и 3-го столбца, поскольку 4-му узлу данного конечного элемента соответствует
глобальный номер 2.
глобальные → |
11 |
7 |
3 |
2 |
1 |
6 |
9 |
10 |
|
|
|
|
|
локальные → |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
[K1,1] |
[K1,2] |
[K1,3] |
[K1,4] |
[K1,5] |
[K1,6] |
[K1,7] |
[K1,8] |
|
|
{F1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
2 |
|
[K2,2] |
[K2,3] |
[K2,4] |
[K2,5] |
[K2,6] |
[K2,7] |
[K2,8] |
|
|
{F 2} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
[K3,3] |
[K3,4] |
[K3,5] |
[K3,6] |
[K3,7] |
[K3,8] |
|
|
{F3} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
[K4,4] |
[K4,5] |
[K4,6] |
[K4,7] |
[K4,8] |
|
|
{F 4} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
|
|
|
|
[K5,5] |
[K5,6] |
[K5,7] |
[K5,8] |
|
|
{F5} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
|
|
|
|
|
[K6,6] |
[K6,7] |
[K6,8] |
|
|
{F 6} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
7 |
|
симметрично |
|
|
|
[K7,7] |
[K7,8] |
|
|
{F 7} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
8 |
|
|
|
|
|
|
|
[K8,8] |
|
|
{F8} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↑ |
↑ |
|
матрица жесткости для I элемента |
|
|
вектор |
|||||||
|
|
|
|
|
|||||||||
глоб. |
лок. |
|
|
|
узловых сил |
||||||||
|
|
|
|
|
|
|
|
||||||
Рис. 7.6
При включении в глобальные матрицы жесткостей и узловых сил для всех последующих конечных элементов соответствующие жесткости и узловые силы должны суммироваться с теми, которые уже были размещены там ранее.
Описанный алгоритм называется сборкой глобальной системы уравнений МКЭ.
65

1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
→ |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K5,5] |
|
[K4,5] |
|
[K3,5] |
|
|
|
[K5,6] |
|
[K2,5] |
|
|
[K5,7] |
|
[K5,8] |
[K1,5] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K4,4] |
|
[K3,4] |
|
|
|
[K4,6] |
|
[K2,4] |
|
|
[K4,7] |
|
[K4,8] |
[K1,4] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K3,3] |
|
|
|
[K3,6] |
|
[K2,3] |
|
|
[K3,7] |
|
[K3,8] |
[K1,3] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K6,6] |
|
[K2,6] |
|
|
[K6,7] |
|
[K6,8] |
[K1,6] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K2,2] |
|
|
[K2,7] |
|
[K2,8] |
[K1,2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K7,7] |
|
[K7,8] |
[K1,7] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K8,8] |
[K1,8] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[K1,1] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓
Рис. 7.7
7.4.Нагрузки и воздействия
ВМКЭ все действующие на тело нагрузки, к которым относятся
• сосредоточенные силы,
• силы, распределенные по поверхности,
• распределенные по объему гравитационные силы
приводятся к эквивалентным системам сил, приложенным в узловых точках.
Покажем как сосредоточенную силу, приложенную в произвольной точке, привести к эквивалентной системе узловых сил.
66
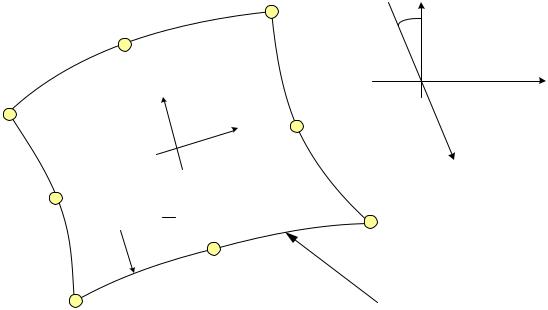
Рассмотрим случай (рис. 7.8), когда сосредоточенная сила приложена в
произвольной точке на одной из сторон плоского квадратичного изопараметрического
элемента.
y
θ
x
η
ξ
η =η |
ξ = ξ P |
|
ξ = +1 |
||
|
P
ξ = −1
Рис.7.8
Дадим виртуальные смещения u* и v* соответственно по осям x и y, узлам, расположенным на рассматриваемой стороне элемента. Тогда для i-го узла можно написать равенства:
Pxiu* = Px Ni (ξp ,η)u*,
(7.39)
Pyiv* = Py Ni (ξp ,η)v*,
где Px и Py компоненты силы Р; ξP ― локальная координата точки приложения силы,
а η― постоянное значение другой локальной координаты, определяющее положение рассматриваемой стороны (+1 или -1).
P |
|
P |
|
||
|
xi |
= N |
(ξP ,η) |
x . |
(7.40) |
|
P |
|
|
P |
|
yi |
|
y |
|
||
Таким же образом с помощью функций формы глобальные координаты точки, в которой приложена сосредоточенная сила, могут быть выражены через координаты узлов:
xP =yP
∑Ni (ξP ,η) xi |
, |
|
3 |
|
|
i=1 |
yi |
(7.41) |
|
|
|
67
где xi и yi - координаты i-го узла рассматриваемой стороны.
Гравитационная сила действует на каждый элементарный объем тела, и ее направление в общем случае может не совпадать с направлением координатных осей x
и y. Ее величина равняется:
dG = ρ g dV,
где ρ ― удельная плотность материала конструкции, g ― ускорение свободного падения.
Компоненты этой силы по осям х |
и у |
соответственно равны: |
|
|
dGx |
= ρ g dV sin θ, |
|
||
dGy |
= −ρ g dV cos θ. |
|
||
Дадим виртуальные смещения |
u* |
и v* в направлении осей х и |
у. В |
|
соответствии с принципом виртуальных работ получим следующие выражения: |
|
|||
Pxiu* = ∫ Ni (ξP ,η)u* ρ g sin θdV , |
(7.42) |
|||
Ve |
|
|
|
|
Pyiv* = −∫ Ni (ξP ,η)v* ρ g cosθdV , |
(7.43) |
|||
|
Ve |
|
|
|
где Ni ― функции формы, а индекс i для рассматриваемого типа конечного элемента изменяется от 1 до 8.
Из формул 7.42 - 7.43 следует матричное выражение для эквивалентных узловых
сил:
Pxi |
= ∫ |
sin θ |
|
|
|
|
N ρ g |
dV. |
|
Pyi |
Ve |
−cosθ |
||
Численное интегрирование может быть выполнено по правилу Гаусса:
Pxi |
N N |
|
sin θ |
,ηm )WnWm det[J ] |
|
|
|
= ∑∑ρ g t |
Ni (ξn |
||
Pyi |
n=1 m=1 |
−cosθ |
|
||
где t ― толщина элемента; [J ] ― матрица Якоби; Wn ,Wm - весовые множители.
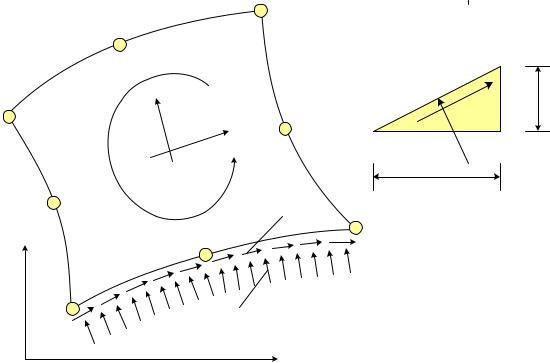
На каждую из сторон конечного элемента в том случае, когда она выходит на поверхность тела, могут действовать распределенные нормальные и касательные внешние силы (рис.7.9).
68
η |
d S |
Pt |
ξ |
d y |
|
|
|
Pn
d x
Pt |
y |
Pn |
x |
Рис.7.9 |
Применение квадратичных конечных элементов позволяет учитывать распределенные воздействия, которые изменяются по квадратичному закону, используя приведение их к сосредоточенным силам, приложенным в узлах конечного элемента.
69
