Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5684

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

647.86 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

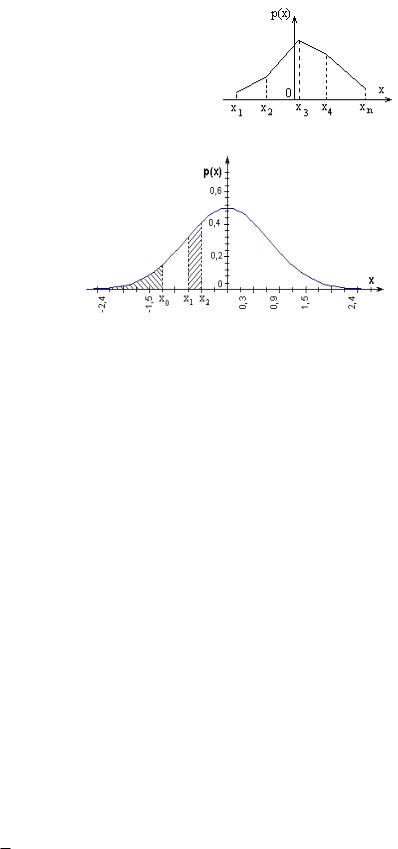
4)Prob(x1<X x2)=P(x2)-P(x1) ;

5)Prob(X=x1)=0. Вероятность обнаружить число, например 241.000... равно 0. Однако, делая измерения, мы округляем значения, тем самым, увеличивая вероятность их

появления. Например, округленное 241.0 содержит значения от 240.9500... до

241.04999... и вероятность попадания числа в этот интервал не равна 0. Распределение с.в. Х характеризуется также функцией

плотности распределения с.в. Для дискретных значений с.в. функция плотности распределения может задаваться таблично. График функции р(х)=рi при x=xi изображен на рис. .

Т.к. возможные значения xi с.в. образуют полную группу несовместных событий (т.е. в каждом из n испытаниях с.в.

обязательно примет				одно		из	значений			xi с определенной
				n
вероятностью),		то		pi 1,		где	n	- число
испытаний.				i 1
испытаний.
	Для непрерывной с.в. функция плотности
распределения имеет вид, показанный на
рисунке.								Р(х)
Если	функция		распределения				с.в.	Р(х)		-
непрерывна, то				p(x)	dP(x)
непрерывна, то				p(x)		dx
						dx
или	p(x) lim		Prob(x X x x)						dP(x)		.
или	p(x) lim										.
	x 0			x					dx
	x 0

По непрерывной кривой плотности распределения, в отличие от дискретной, вероятность обнаружить точное число х2 равна нулю. При помощи функции р(х) вероятность обнаружить с.в. Х в бесконечно малом интервале x<X<x+dx равна Prob(x<X<x+dx)=p(x)dx (площадь прямоугольника, dx 0). То же в конечном интервале x1<X<x2:

Prob(x1 X x2 ) p(x)dx

(Геометрически это заштрихованная площадь под кривой плотности распределения).

Итак P(x) p(x)dx,

поэтому функцию распределения называют еще интегральной функцией распределения. Свойства функции плотности распределения:

1) Плотность распределения вероятностей - неотрицательная функция р(х) 0.

2) p(x)dx 1,

что эквивалентно Р( )=1.

3)Размерность р(х) обратная размерности с.в., а Р(х) - безразмерна.

4)Числовые характеристики распределения

Математическое ожидание с.в. Х : - дискретной

	m
	M(x) xi pi
	i 1
m
при этом pi 1	(М(x) - случайна при n ).

i 1

- непрерывной

X xp(x)dx,

Математическое ожидание X - достоверная величина, т.к. вероятность того, что при n= испытаниях мы получим среднее арифметическое М(X)= X равна 1.

М(с)=с, М(сx) = сМ(x), где с – неслучайное число. Для независимых с.в. Х1 и Х2

М(x1+x2)=М(x1)+М(x2), М(x1x2)=М(x1)М(x2), М(x2)=[М(x)]2+D(x).

К математическому ожиданию стремится среднее арифметическое наблюдаемых значений с.в. при количестве испытаний n . Геометрически м.о. – это абсцисса ц. т. площади под кривой плотности распределения. Размерность м.о. совпадает с размерностью с.в.

Дисперсия с.в. Х - м.о. квадрата отклонения с.в. Х от ее м.о. (центра распределения):

D(x)=M[x-M(x)]2=M(x2)-M2(x),

т.к. M[x-M(x)]2=M[x2-2xM(x)+M2(x)]=M(x2)-2M2(x)+M2(x), M[2xM(x)]=2M2(x) и M[M(x)]=M(x).

Дисперсия дискретной с.в. Х

D(x) (xi M(x))2 pi

i 1

случайна при n .

Дисперсия непрерывной с.в. Х:

D(x) (x X)2 p(x)dx x2 p(x)dx x2 ,


(дисперсия непрерывной с.в. - достоверна).
D(x) M[(x		)2 ], при		0	D(x) M(		2 ),		- математическое ожидание.
	X		X			X		X

Дисперсия характеризует разброс с.в. вокруг ее среднего значения (математического ожидания).

D(c)=0, D(cx)=c2D(x), D(c+x)=D(x).

Доказательство.

D(cx)=M[cx-M(cx)]2=M[c2x2-2cxM(cx)+M2(cx)]= c2M(x2)-M[2c2xM(x)]+M[c2M2(x)]= c2M(x2)-2c2M2(x)+c2M2(x)= c2[M(x2)-M2(x)]=c2D(x). D(c+x)= M[c+x-M(c+x)]2=M[c+x-c-M(x)]2=M[x-M(x)]2=D(x).

Для независимых с.в. Х1 и Х2 D(x1±x2)=D(x1)+D(x2).

Геометрически дисперсия – это центральный момент инерции площади под кривой плотности распределения. Размерность дисперсии - квадрат размерности с.в.

Среднеквадратическое отклонение (стандарт): (x) D(x) .

Асимметрия непрерывной с.в. Х:

A(x) (x X)3 p(x)dx.

Если с.в. Х распределена симметрично относительно своего м.о., то А(х)=0.

Коэффициент изменчивости (вариации) с.в. Х - отношение стандарта к м.о.:

V(x) (x)/ X 1.

3.2. Функции случайных величин

Функция с.в. будет также случайной величиной Y= (X). Ее распределение соответствует распределению аргумента, но с измененной шкалой абсцисс. P(y)=Prob(Y<y)=Prob( (X)<y).

P(y) p[ (y)] (y) dy ,

где (y) - функция обратная (х) (замена подинтегрального выражения x= (y), dx= (y)dy). Если Y= (X), где (X) - монотонная функция своего аргумента, то распределение Y определяется тем, что вероятность нахождения y в пределах y1<Y<y2 равна вероятности

неравенства х1<X<x2,

где y1= (x1) и y2= (x2).

М.о. и дисперсия с.в. Y:

							)2 p(x)dx.
		(x)p(x)dx,
	Y	(x)p(x)dx,		D(Y) ( (x) Y



Y yp(y)dy,			y (x) dy		(x)dx,
Y yp(y)dy,			y (x) dy		(x)dx,	(40) p(y) p(x) (y)

Y (x)p(x) (y) (x)dx.

4. НЕКОТОРЫЕ НАИБОЛЕЕ ВАЖНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

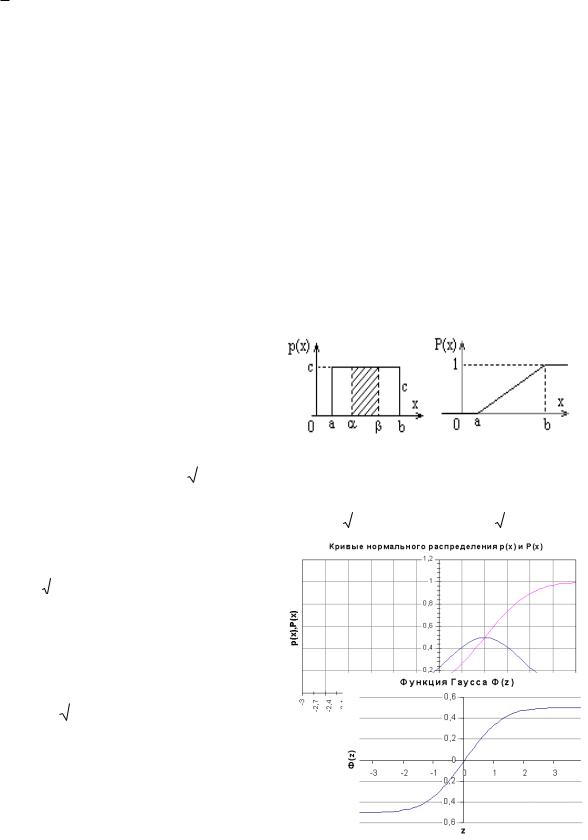
4.1. Равномерное распределение вероятностей

Для него вероятность того, что с.в. Х попадет в интервал Х : Prob( Х )=( - )/(b-a).

Функция распределения	P(x)	x a	,	a<x<b.

		b a

0, x a;

Функция плотности распределения (вероятности): p(x) c, a x b;

0, x b.

М.о. и дисперсия: M(x)

a b

D(x)

(b a)2

4.2.Нормальное распределение

Плотность распределения:

p(x)

exp

(x)

(x) 2

Точки перегиба кривой плотности распределения:

(x);

и X (x);

(x)

Функция распределения:

P(x)

exp

dx,

(x)

где

- м.о., (х) – стандарт.

Чем больше (х), тем ниже и шире кривая плотности

распределения.

Плотность n-мерного

нормального распределения:

p(x1,x2,...,xn )

exp

Ajl (xj

X j )(xl

(2 )

n/2

2 j, l 1

, где - определитель корреляционной матрицы

kjl

, а Ajl –

алгебраическое дополнение элемента kjl-того определителя.

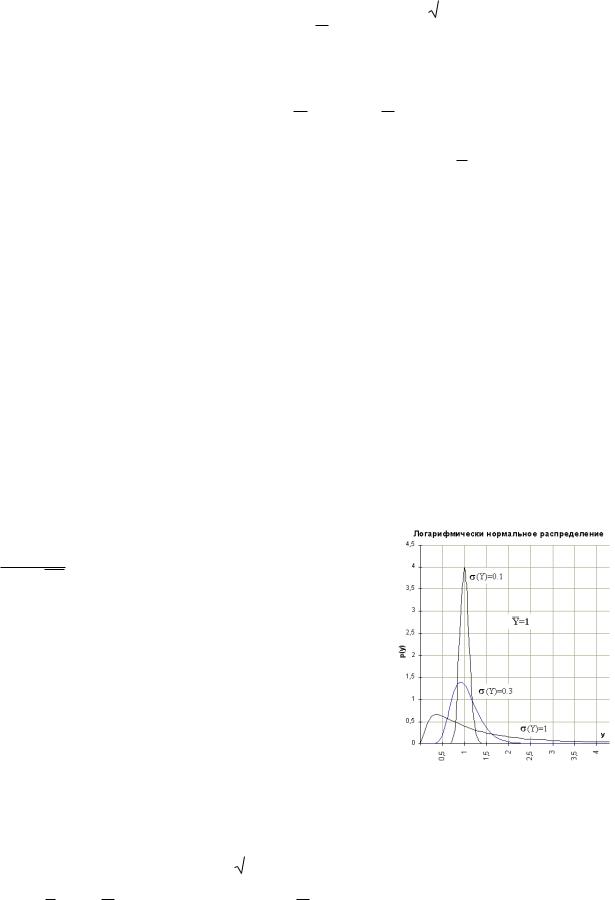
Р(х) можно выразить через интеграл вероятности Гаусса

	1		z
Ф(z)			exp( 0.5z2 )dz,

	2
		0

1	x X
P(x)	Ф

2
		(x)

Функция – нечетная (Ф(-z) = - Ф(z)), имеются таблицы ее значений. Вероятность попадания с.в. Х в интервал (a,b) –

b X			a X
Prob(a x b) Ф		Ф


	(x)			(x)

Если b-a =6 (X), то вероятность того, что с.в. Х окажется в интервале X 3 (X) равна

0.9973. Линейные функции с.в., подчиняющиеся нормальным законам распределения, имеют также нормальный закон распределения.

Как показал Ляпунов в случае, если число n безгранично увеличивается, кривая плотностей вероятностей суммы не зависит от кривых плотностей вероятностей, слагаемых при некоторых предположениях, и представляет собой нормальную кривую.

Условия: слагаемые величины х=х1+х2+...+хn (xi, i=1, 2...n) в среднем одного порядка и одного порядка некоторые характеристики слагаемых - вторые и третьи моменты. Т.о. если с.в. образуется из суммы большого числа независимых, неограниченных случайных переменных факторов, то ее закон - близок к нормальному, т.е. в действительности многие переменные представляют собой результат простого суммирования многих независимых факторов.

Закон больших чисел:

Prob(X x)

, Prob

D(X)

(Prob(X 0) 0.

4.3. Усеченный нормальный закон

Если известны границы возможных значений с.в. (a,b), то

pc (x)

p (x)c

(x)2

0, x a,

(x X)2

exp

(x)

a x b

(x)

x b.

Закон используется для описания реальных величин, распределенных нормально (например, не могущих принимать отрицательные значения).

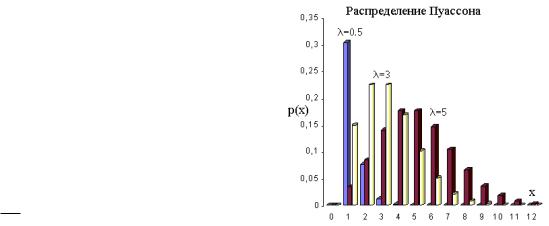
4.4. Логарифмически нормальное распределение

Если некоторая с.в. Х распределена по нормальному закону (45.4), то ее экспоненциальная функция

Y=exp(X)

(X=ln(Y)) распределится по закону:


p(y) p(x)	dx	1			(ln y X)2				y e	x
				exp				,
						2	(x)
			2		2	2
	dy y (x)		2		2

М. о. и дисперсия:

Y exp X 0.5 2 (x) , D(Y) exp 2X D(X) exp D(X) 1

Коэффициент вариации: V(Y) exp D(x) 1. Изменению Х по нормальному закону в пределах (- , ) соответствует изменение Y (0,+ ).

4.5.Распределение Вейбулла

В теории хрупкого разрушения и других отраслях техники нашло применение распределение Вейбулла. Интегральная кривая распределения:

P(x) 1 exp( cxb ), c 0, b 0, 0 x

Плотность распределения:

p(x) exp( cxb )b( cxb 1) bcxb 1 exp( cxb )

В выражения для числовых характеристик распределения Вейбулла входит гамма-функция

Г( ) x 1e xdx,

которая табулирована в математических справочниках.

4.6.Распределение Гумбеля (двойное экспоненциальное распределение)

Используется при статистическом анализе снеговых и ветровых нагрузок на сооружения. Функция распределения (интегральная):

		x
P(x) exp	exp

Значению x= соответствует вероятность непревышения , равная

P( )=exp(-exp0))=exp(-1)=1/e=0.36788.

Значению x=0 соответствует вероятность непревышения 0, равная P(0)=exp[-exp( / )]. Плотность распределения:

p(x)

exp

- <x< , - < < , >0.

Если возвести в n-ную степень, то интегральная кривая не изменит своего вида, а только сместится вдоль оси на величину ln(n):

Pn (x) e

Параметры и

x lnn

lnn

x lnn

exp

связаны с м.о. X и дисперсией D(x):

X 0.5776 , D(X) 1.645 2 .

4.7. Распределение максимумов случайных величин

Рассматривается n статически независимых с.в. Xi (i = 1, 2, …, n) и имеется вероятность того, что ни одна из них не превысит х. Вероятность непревышения значения х величиной Xi Prob(Xi<x)=Pi(x),

где Pi(x) – интегральный закон распределения Xi. Вероятность непревышения х ни одной из величин Xi:

Pn (x) Pi (x),

i 1

где Pn(x) – интегральный закон распределения максимумов совокупности n с.в. Xi. Тогда плотность распределения вероятностей:

	n
	d Pi (x)	n	n	p (x)
pn (x)	i 1	Pi (x)		i	.
pn (x)	dx	Pi (x)		Pi (x)	.
	dx	i 1	i 1	Pi (x)

Для 3-х с.в.

p3(x) p1(x)P2(x)P3(x) P1(x)/P1(x) P1(x)p2(x)P3(x) P2(x)/P2(x) P1(x)P2 (x)p3(x) P3(x)/P3(x)

	p1(x)	p2(x)	p3(x)

	P(x)	P(x)	P(x)
P1(x)P2 (x)P3(x)				.
	1	2	3

Если закон распределения всех с.в. Xi одинаков, то

Pn (x) Pn (x), pn (x) nPn 1(x)p(x),

где Pn(x) и pn(x) – интегральная функция распределения и плотность распределения максимумов, получаемых при n реализациях одной и той же с.в. Xi.

М.о. и дисперсия максимума в n опытах:


						n xpn (x)dx n xPn 1(x)p(x)dx,
					X	n xpn (x)dx n xPn 1(x)p(x)dx,

D (x)	(x		)2 p	(x)dx n			(x		n )2	Pn 1(x)p(x)dx.
D (x)	(x	X	)2 p	(x)dx n			(x	X	n )2	Pn 1(x)p(x)dx.
n			n

4.8. Распределение Пуассона

Это дискретное распределение описывает число событий, происходящих в одинаковых промежутках времени при условии, что события происходят независимо одно от другого с постоянной интенсивностью. Вероятность того, что с.в. Х примет значение, равное m (m

– целое число):

p e , 0, m 0,1,2,3...

m m!

Распределение зависит от одного параметра , называемого пуассоновским потоком. Существуют некоторые недостатки при описании реальных с.в.: так в некоторых

законах с.в. может принимать отрицательные значения (нормальный закон), хотя этими законами описываются изначально только положительные величины (предел текучести стали и т.д.). Кроме того, теоретические распределения допускают, хотя и с малой вероятностью, возможность сколь угодно больших отклонений с.в. от среднего значения.

Все теоретические закономерности и законы теории вероятностей относятся к идеальным схемам. Применяемые обычно теоретические законы распределения относятся к ситуациям с неограниченным нарастанием числа случайных факторов или с неограниченным повторением некоторого явления и имеют характер предельных закономерностей, к которым приближаются реальные распределения.

Кроме перечисленных используются и другие распределения – Пирсона 3-го рода, Рэлея, Максвелла, Пирсона 2-го рода, 2 (хи-квадрат), Стьюдента, Фишера и т.д.

5.СЛУЧАЙНЫЕ ФУНКЦИИ

5.1.Характеристики случайных функций

Случайная функция – функция, которая в результате опыта может принять тот или иной неизвестный заранее конкретный вид. Обычно аргументом случайной функции (с.ф.) является время, тогда с.ф. называют случайным процессом (с.п.).

С.ф. непрерывно изменяющегося аргумента t называется такая с.в., распределение которой зависит не только от аргумента t=t1, но и от того, какие частные значения принимала эта величина при других значениях данного аргумента t=t2. Эти с.в. корреляционно связаны между собой и тем больше, чем ближе одни к другим значения аргументов. В пределе при интервале между двумя значениями аргумента, стремящемся к нулю, коэффициент корреляции равен единице:

r(X	, X		)	k(X1, X2 )	1,

1		2	(X1) (X2 )

т.е. t1 и t1+ t1 при t1 0 связаны линейной зависимостью.

С.ф. принимает в результате одного опыта бесчисленное (в общем случае несчетное) множество значений – по одному для каждого значения аргумента или для каждой совокупности значений аргументов. Эта функция имеет одно вполне определенное значение для каждого момента времени. Результат измерения непрерывно изменяющейся величины является такой с.в., которая в каждом данном опыте представляет собой определенную функцию времени.

С.ф. можно также рассматривать как бесконечную совокупность с.в., зависящую от одного или нескольких непрерывно изменяющихся параметров t. Каждому данному значению параметра t соответствует одна с.в Xt. Вместе все с.в. Xt определяют с.ф. X(t). Эти с.в. корреляционно связаны между собой и тем сильнее, чем ближе друг к другу.

Элементарная с.ф. – это произведение обычной с.в. Х на некоторую неслучайную функцию (t): X(t)=X (t), т.е. такая с.ф., у которой случайным является не вид, а только ее масштаб.

С.ф. Y(t) X(t) X(t) - имеет м.о. равное нулю. p[x(t1)] – плотность распределения с.в. Х (значения с.ф. X(t)), взятой при произвольном значении t1 аргумента t.

Реализация с.ф. X(t) – описывается уравнением x=f1(t) при t=t1 и уравнением x=f2(t) при t=t2.

Вообще функции x=f1(t) и x=f2(t) – различные функции. Но эти функции тождественны и линейны тем более, чем более (t1 t2) t1 ближе к t2.

Одномерная плотность вероятности с.ф. p(x,t) – зависит от х и от параметра t. Двумерная плотность вероятности p(x1,x2;t1,t2) – совместный закон распределения значений X(t1) и X(t2) с. ф. X(t) при двух произвольных значениях t и t аргумента t.

	p x ,x						dx			p x (t ),x				) dx	.
p(x ,t )	p x ,x	2	;t	1	,t	2	dx	2	p(x (t ))	p x (t ),x	2	(t	2	) dx	.
1 1	1	2		1		2		2	1 1	1 1	2		2		2

В общем случае функция X(t) характеризуется большим числом n-мерных законов распределения p x(t1),x(t2 ),...,x(tn ) .

М.о. с.ф. X(t) - неслучайная функция X(t) , которая при каждом значении аргумента t равна м.о. ординаты с.ф. при этом аргументе t.

X(t) x(t1)p x(t1) dx(t1), p x(t1) - функция, зависящая от x и t.

Аналогично и дисперсия - неслучайная функция.

Степень зависимости с.в. для различных значений аргумента характеризуется автокорреляционной функцией.

Автокорреляционная функция с.ф. X(t) - неслучайная функция двух аргументов Kx(ti,tj), которая при каждой паре

значений ti, tj равна корреляционному моменту соответствующих ординат с.ф. (при i=j корреляционная функция (к.ф.) обращается в дисперсию с.ф.);

Kx (t1,t2 ) x(t1) X(t1) x(t2 ) X(t2 ) p x(t1),x(t2) dx(t1)dx(t2 ),

где p x(t1),x(t2 ) - совместная плотность распределения двух с.в. (значений с.ф.), взятых при двух произвольных значениях t1 и t2 аргумента t. При t1=t2=t получаем дисперсию D(t).

X(t)

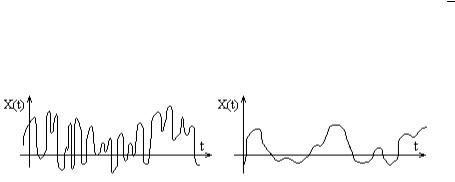
Автокорреляционная функция - совокупность м.о. произведений отклонений двух ординат с.ф. X(t) , взятых при аргументах t1 и t2, от ординат неслучайной функции м.о. , взятых при тех же аргументах.

Автокорреляционная функция характеризует степень изменчивости с.ф. при изменении аргумента. На рис. видно, что зависимость между значениями с.ф., соответствующим двум данным значениям аргумента t - слабее в первом случае.

Рис. Корреляционно связанные случайные функции

Если две с.ф. X(t) и Y(t), образующие систему не являются независимыми, то тождественно не равна нулю их взаимная корреляционная функция:

x(t )

(t ) y(t

) p x(t ), y(t

) dx(t )dy(t

) ,

,t ) K

(t ,t

)

) Y

p x t1 , y t2

где

- совместная плотность распределения двух с.в. (значений двух с.ф. X(t) и

Y(t)), взятых при двух произвольных аргументах (t1 - аргумент функции

X(t), t2 - аргумент функции Y(t)).

Если X(t) и

Y(t)

независимы,

то KXY(t1,t2)=0.

Система из n с.ф.

X1(t),

X2(t),...,Xn(t)

характеризуется

м.о.

1(t),

2 (t),...,

n (t),

n автокорреляционными

функциями

KX1

t1,t2 ,KX2 t1,t2 ,..., KXn t1,t2

еще

n(n-1)/2

корреляционными

функциями

KX1X2 t1,t2 ,..., KXn 1Xn t1,t2 .

Взаимная корреляционная функция (характеризует связь между двумя с.ф., т.е. стохастическую зависимость) KXY ti ,tj двух с.ф. X(t) и Y(t) - неслучайная функция двух

аргументов ti и tj, которая при каждой паре значений ti, tj равна корреляционному моменту соответствующих сечений с.ф. Она устанавливает связь между двумя значениями двух функций (значения - с.в.), при двух аргументах t1 и t2.

Особое значение имеют стационарные случайные функции, вероятностные характеристики которых не меняются при любом сдвиге аргумента. М.о. стационарной с.ф. постоянно (т.е. не является функцией), а корреляционная функция зависит лишь от разности значений аргументов ti и tj.

		(t) const	KX ti ,tj KX KX , ti tj
	X
Это четная функция (симметрично OY).

Из (69.5) KX ti ,tj D(t) const, KX 0	KX	( )	.

При большом значении интервала времени =t2-t1		отклонение ординаты с.ф. от ее м.о. в

момент времени t2 становится практически независимым от значения этого отклонения в момент времени t1. В этом случае функция KX( ), дающая значение корреляционного момента между X(t1) и X(t2), при стремится к нулю.

Многие стационарные с.ф. обладают эргодическим свойством, которое заключается в том, что при неограниченно возрастающем интервале наблюдения среднее наблюденное значение стационарной с.ф. с вероятностью, равной 1, будет неограниченно приближаться к ее м.о. Наблюдение стационарной с.ф. при разных значениях t на достаточно большом интервале в одном опыте равноценно наблюдению ее значений при одном и том же значении t в ряде опытов.

Иногда требуется определить характеристики преобразованных с.ф. по характеристикам исходных с.ф. Так если

t		dx(t)
Z(t) x(t)dt;	y(t)		,

0		dt

t
то Z(t) X(t)dt; Y (t) dX(t) т.е. м.о. интеграла (производной) от с.ф. равно интегралу
0	dt

(производной) от м.о. (y(t) - скорость изменения с.ф. X(t), Y (t) - скорость изменения м.о.).

При интегрировании или дифференцировании с.ф. получаем также с.ф. Если X(t)

распределена

нормально,

то Z(t) и Y(t)

распределены тоже нормально.

Если X(t) –

стационарная с.ф., то Z(t) уже не стационарная с.ф., т.к. DZ (t) 2 (t )KX ( )d

зависит от t.

Примеры корреляционных функций.

Kx ( ) 2e

(из (2) при );

( ) 2e

cos

sin

;

3) Kx( ) 2e 2	cos ;	4) Kx( ) 2e	cos ;

5)Kx( ) 2e 2	(из (3) при );	6) Kx( ) 2e		(из (4) при ).


На графиках = 1, = 5, = 1.

- характеризует быстроту убывания корреляционной связи между ординатами с.ф. при увеличении разности аргументов этих ординат .

- характеризует "степень нерегулярности процесса". При малом ординаты процесса оказываются сильно коррелированными и реализация процесса похожа на синусоиду; при большом периодичность с частотой становится незаметной.

Корреляционные функции 4 и 6 – не имеют производных при =0. Соответствующие спектральные плотности:

2) S( )			2 2				2 2 2						;
2) S( )					( 2 2 2 )2 4 2 2								;
					( 2 2 2 )2 4 2 2
3)				2				( )		2				( )		2	;
								( )						( )
	S( )								2						2
	S( )				exp			4	2		exp			4	2
			4					4						4
4) S( )		2				2 2 2						;
4) S( )												;
			( 2 2 2 )2 4 2 2
6) S( )			2				.
6) S( )				2			.
				2	2

Чтобы найти корреляционную функцию интеграла (производной) от с.ф., нужно дважды проинтегрировать (продифференцировать) корреляционную функцию исходной с.ф. сначала по одному, затем по другому аргументу:

ti tj

KZ (ti ,tj ) KX (ti ,tj )dtidtj
		0 0		.
			2KX (ti ,tj )	.
			2KX (ti ,tj )
KY	(ti	,tj )
KY	(ti	,tj )	ti tj
			ti tj

Формула для стационарной функции примет вид:

) K

( )

d2K

( )

; t

( )

d2K

( )

d 2

Корреляционная

функция

с.ф.

и ее

производной KXY

( )

dKX ( )

. Для

дифференцируемого стационарного процесса ордината с.ф. и ее производной, взятая в тот же момент времени являются некоррелированными с.в. (а для нормального процесса и независимыми).

При умножении с.ф. на детерминированную получаем с.ф. Z(t)=a(t)X(t), корреляционная функция которой равна

KZ(t1,t2)=a(t1)a(t2) KX(t1,t2) ,

где a(t) - детерминированная функция.

Сумма двух с.ф. является тоже с.ф. Z(t)=X(t)+Y(t) и ее корреляционная функция при наличии корреляционной связи между X(t) и Y(t):

KZ(t1,t2)=KX(t1,t2)+ KY(t1,t2)+2KXY(t1,t2),

где KXY(t1,t2) - см. (68.5) - взаимная корреляционная функция двух зависимых с.ф. X(t) и Y(t).

Если X(t) и Y(t) независимы, то KXY(t1,t2)=0. М.о. с.ф. Z(t):

Z(t) X(t) Y(t) .

5.2. Выбросы случайной функции за заданный уровень

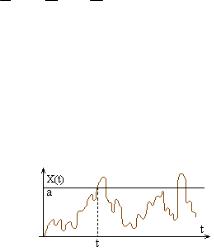
Необходимость определения вероятностных характеристик процесса пересечения с. функцией заданного уровня возникает, когда необходимо вычислить вероятность того, что в течение срока службы нагрузка, действующая на строительную конструкцию, не превысит допустимого уровня. Найдем вероятность пересечения случайной функцией (дифференцируемой) X(t) некоторого уровня а в течение времени t.

Полагая скорость изменения с.ф. V(t)=dX(t)/dt постоянной в течение времени dt (с точностью до бесконечно малых второго порядка) условие пересечения функцией X(t) уровня а за малый промежуток времени dt:

X(t)<a; X(t)+V(t)dt>a

или

a-V(t)dt<X(t)<a (V(t)>0) .

Вероятность этого события (выраженного условием (75)):

Qa (t) p(x,V)dxdV ,

0 a Vdt

где p(x,V) - совместная плотность распределения с.ф. X(t) и V(t).

Ввиду близости пределов внутреннего интеграла (его заменили на p(a,V)Vdt - площадь прямоугольника) вероятность выброса:

Qa (t) dt p(a,V)VdV .

Если разделить вероятность выброса Qa на время dt, в течение которого он ожидается,

получится временная плотность вероятности выброса за уровень а в момент t (среднее число выбросов в единицу времени):

q(a) p(a,V)VdV .

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023131.42 Кб0568.pdf
#
21.11.2023647.38 Кб05680.pdf
#
21.11.2023647.51 Кб05681.pdf
#
21.11.2023647.51 Кб05682.pdf
#
21.11.2023647.71 Кб05683.pdf
#
21.11.2023647.86 Кб05684.pdf
#
21.11.2023647.99 Кб05685.pdf
#
21.11.2023648.03 Кб15686.pdf
#
21.11.2023648.26 Кб05687.pdf
#
21.11.2023648.35 Кб05688.pdf
#
21.11.2023648.38 Кб15689.pdf