
3457
.pdf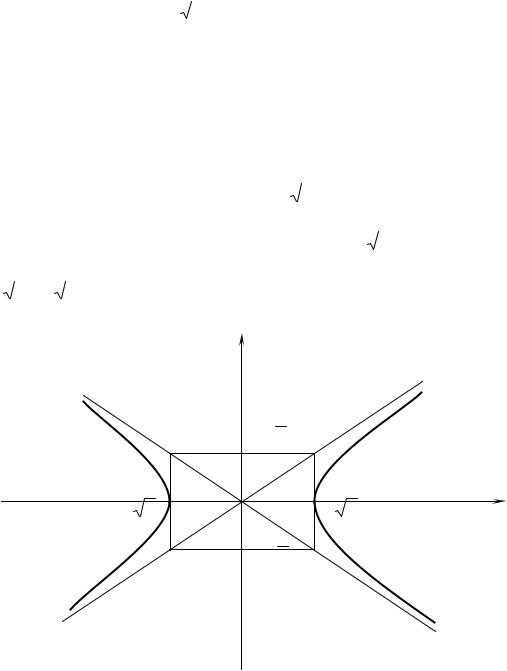
8. Уравнение |
x2 |
- |
|
y 2 |
= -1 задает гиперболу, сопряженную к (10). Для |
||||||||||||||||||||||||
a2 |
|
b2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сопряженной гиперболы b |
– действительная полуось, |
a – |
мнимая |
||||||||||||||||||||||||||
полуось. Она расположена в области |
|
y |
|
³ b .(на рис. |
6 |
изображена |
|||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
пунктиром). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
«Вырождения» гиперболы: |
|
|
|
|
|
|
|
|||||||||||
|
x 2 |
y 2 |
x |
|
|
y x |
|
y |
x |
|
y |
|
|
x |
|
y |
|
||||||||||||
|
|
- |
|
= 0 , |
|
|
- |
|
|
|
+ |
|
= 0 отсюда |
|
- |
|
= 0 |
и |
|
+ |
|
= 0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
a 2 |
b 2 |
a |
|
|
b a |
|
b |
a b |
|
|
a b |
|
||||||||||||||||
или y = |
b |
x и |
y = - |
b |
x – |
пара пересекающихся прямых. |
||||||||||||||||
|
|
|||||||||||||||||||||
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Точка M (6,-2 |
|
|
) лежит на гиперболе, уравнения асимптот |
|||||||||||||||||||
|
2 |
|||||||||||||||||||||
которой y = ± |
2 |
x . Составить уравнение гиперболы и построить ее. |
||||||||||||||||||||
|
||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Каноническое уравнение гиперболы |
x2 |
- |
y 2 |
=1, т.к. |
||||||||||||||||||
a2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
||
асимптоты y = ± |
2 |
x , то |
b |
= |
2 |
|
, b = |
2 |
a . Подставим последнее в уравнение |
|||||||||||||
3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
a |
3 |
|
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x2 |
- |
y 2 |
× 9 =1, далее т. M (6,-2 |
|
) лежит на |
||||||||||||||
гиперболы: |
2 |
|||||||||||||||||||||||||
a2 |
4a2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
36 |
- |
|
8 × 9 |
=1, |
|
144 - 72 |
=1, 72 = 4a2 , a2 =18 , |
a = 3 |
|
|
||||||||||||||||
|
2 |
; |
||||||||||||||||||||||||
|
a 2 |
4a 2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4a 2 |
|
|
|
|
|
|
|
|
|
|
|
||||
b = |
2 |
× 3 |
|
|
= 2 |
|
|
|
. Итак, искомое уравнение |
x2 |
|
- |
y 2 |
=1. |
|
|||||||||||
2 |
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
18 |
|
8 |
|
|
|
|||||||
y
2
 2
2
- 3 2 |
3 2 |
- 2
 2
2
гиперболе, т.е.
тогда
x
Рис. 7.

§ 5.Парабола. Каноническое уравнение параболы
Параболой называется множество, состоящее из всех точек плоскости, для которых расстояние до некоторой фиксированной точки F , называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой (не содержащей т. F ).
Пусть p – расстояние от F до директрисы. По определению пара-
болы |
|
MF |
|
= |
MN |
|
, |
|
|
|
|
(11) |
|
где точка M – |
произвольная точка параболы, N – |
ее проекция на дирек- |
|||||||||||
трису. Выберем систему координат так, чтобы т. F |
|
p |
,0 |
|
была фокусом, а |
||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
x = − p – директрисой. 2
y
N |
M(x,y) |
− |
p |
0 |
F |
p |
,0 |
|
x |
|
|
|
|
||||
|
|
|
|||||
2 |
|
2 |
|
|
|||
Рис. 8.
Запишем соотношение (11) в координатах:
|
p |
2 |
2 |
|
|
p 2 |
||
x − |
|
|
+ y |
|
= |
x + |
|
|
|
|
|
||||||
|
2 |
|
|
|
|
2 |
||
это и есть уравнение параболы. После упрощения получим: y 2 = 2 px
Уравнение (13) называется каноническим уравнением параболы. Основные характеристики параболы:
(12)
(13)
1.Парабола (13) симметрична относительно оси ox .
2.Точка O(0,0) – вершина параболы (13).
3.Фокальный радиус точки M(x,y) параболы: FM = x + p .
2

Уравнение вида y2 = −2 px (14) определяет параболу, для которой x ≤ 0 , т.е. график этой параболы:
y
M(x,y)
|
− |
p |
|
0 |
p |
x |
|
F |
|
,0 |
|
|
2 |
|
|
2 |
|
|
|||||
|
|
|
|
|
|
||
Рис. 9. |
|
|
|
Уравнения вида |
x2 |
= 2 py |
(15) |
|
x2 |
= −2 py |
(16) |
задают параболы симметричные относительно оси oy :
|
|
|
|
|
|
|
|
p |
y |
|||
|
|
|
|
|
|
|
|
|
N |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
p |
|
|
|
0 |
|
x |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
F 0, |
|
|
|
|
|
|
|
p |
M |
|||
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
M |
|
|
F 0,− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
− p N
2
Рис. 11.
Рис. 10.
|
|
|
«Вырождения» параболы: |
1. |
x2 |
= −k 2 , |
y 2 = −k 2 . Эти уравнения не определяют никакого точечно- |
|
го множества при k ¹ 0 . |
||
2. |
x2 |
= k 2 , |
y2 = k 2 , эти уравнения определяют пару параллельных пря- |
мых: x = ±k и y = ±k . При k = 0 эти прямые совпадают.
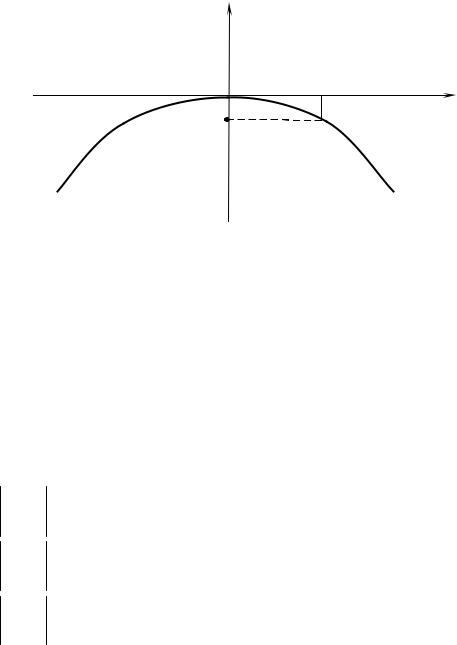
Пример. Парабола, симметричная относительно оси oy , имеет вершину в начале координат и проходит через точку (6,-2). Написать уравнение параболы и определить координаты ее фокуса.
Решение. Уравнение параболы, симметричной относительно оси oy : x2 = 2 py либо x2 = -2 py . Подставим координаты точки в оба уравнения:
62 ¹ 2 p × (- 2), т.к. p > 0 . |
62 = -2 p × (- 2) |
|
36 = 4 p |
|
p = 9 |
Уравнение параболы x2 = -18y , ветви вниз и F (0;−4,5)
y
0 |
6 |
x
-2
F(0;-4,5)
Рис. 12.
§ 6. Применение преобразования координат к приведению уравнений кривых второго порядка к каноническому виду
Значения коэффициентов A, B,C общего уравнения (1) кривой II-го порядка Ax2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0 определяют, к какому типу относится кривая (эллиптическому, гиперболическому или параболическому). Так, например, если A = C и B = 0 , то кривая – окружность или ее «вырождения». В общем случае, если:
A B
1.= AC - B2 > 0 , то кривая эллиптического вида.
B C
2.A B = AC - B2 < 0 , то кривая гиперболического вида.
B C
3.A B = AC - B2 = 0 , то кривая параболического вида.
B C

С помощью преобразований параллельного переноса и поворота координатных осей общее уравнение кривой II-го порядка можно привести к каноническому виду.
Рассматриваются следующие преобразования координат: 1) параллельный перенос координатных осей:
y y′
M
|
|
o′(a,b) |
x′ |
o |
|
|
x |
Рис. 13. |
|
|
|
M (x, y) – |
точка с координатами в старой системе координат oxy , |
||
M (x′, y′) – точка с координатами в новой системе координат o′x′y′, |
|||
O′(a,b) – |
начало координат новой системы с координатами в старой |
||
системе. |
|
|
|
x = x′ + a |
формулы параллельного переноса координатных осей, |
||
|
– |
||
y = y′ + b |
|
|
|
выражающие старые координаты через новые. |
|||
x′ = x − a |
обратные формулы. |
|
|
|
– |
|
|
y′ = y − b |
|
|
|
2) Поворот координатных осей на угол α : |
|||
|
|
y |
|
y′ |
|
M |
x′ |
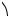 α
α
0 |
x |
|
Рис. 14.
M (x, y) – точка с координатами в старой системе координат oxy , M (x′, y′) – точка с координатами в новой системе координат o′x′y′.
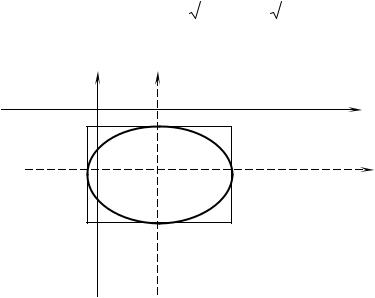
x = x′ × cosα - y′ × sinαy = x¢ × sinα + y¢ × cosα
при повороте осей на угол α .
x′ = x × cosα + y × sinαy¢ = -x × sinα + y × cosα
–формулы преобразования координат т. M
–обратные формулы.
Пример 1. С помощью параллельного переноса осей координат привести к простейшему виду уравнение кривой x2 + 2 y 2 − 4x + 8 y − 10 = 0 и построить ее.
Решение. AC − B2 = 2 > 0 – кривая эллиптического типа. Преобразу-
ем данное уравнение – сгруппируем полные квадраты x2 − 4x + 4 − 4 + 2(y 2 + 4 y + 4 − 4)− 10 = 0
|
|
|
(x - 2)2 + 2(y + 2)2 = 22 |
|
|
|
|
|
|
||||
|
|
|
(x − 2)2 |
+ (y + 2)2 |
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
22 |
11 |
|
|
|
|
|
|
|
|
|
|
|
Положим x − 2 = x′ |
эта система задает формулы параллельного пе- |
|||||||||
|
|
|
|
|
y + 2 = y′ |
|
т. O1 (2,−2). |
|
|
|
|||
реноса |
осей |
координат |
в |
Получим уравнение эллипса: |
|||||||||
|
x12 |
+ |
y12 |
= 11, |
|
a = |
|
, b = |
|
|
|
||
|
с полуосями |
22 |
11 и центром симметрии в |
||||||||||
22 |
|
||||||||||||
11 |
|
|
|
|
|
|
|
|
|
|
|||
т. O1 (2,−2). |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
y |
0 |
|
y′ |
|
|
|
||
|
|
|
|
|
|
|
b |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
-a |
|
|
O1 |
|
|
x′ |
||
|
|
|
|
|
|
|
|
|
a |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
-b
Рис. 15.
Замечание. С помощью параллельного переноса координатных осей удается в общем уравнении избавиться от слагаемых, содержащих x и y в первой степени.
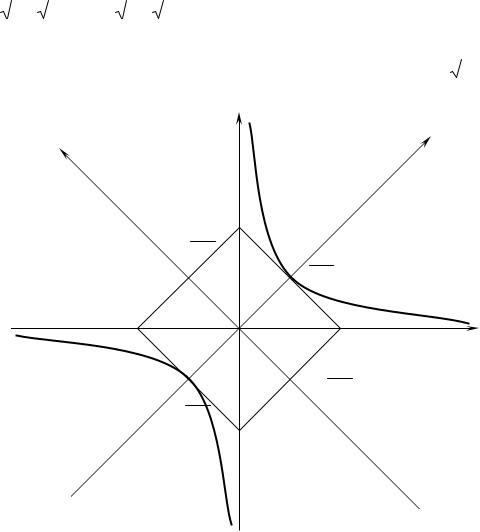
Пример 2. Преобразовать уравнение xy = m (m > 0) к простейшему
виду.
Решение: AC − B2 = −1 < 0 – кривая гиперболического типа. Повернем заданную систему координат на угол α .
Подставим в заданное уравнение формулы
x = x′× cosα - y′ |
× sinα |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = x¢ × sinα + y¢ × cosα |
|
|
|
|
|
|
|
||||||||||||||
(x′cosα − y′sinα)(x′sinα + y′cosα)= m |
|
|
|
||||||||||||||||||
|
x′2 cosα sinα − y′2 sinα cosα + x′y′(cos2 α − sin 2 α)= m |
||||||||||||||||||||
cos2 α − sin 2 α = 0 , |
cos 2α = 0 , |
2α = π , |
α = π . |
||||||||||||||||||
Итак, при α = π |
|
|
|
|
|
|
|
2 |
4 |
|
|
||||||||||
мы избавились в уравнении от слагаемого, содер- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
жащего произведение x′× y′ и получили уравнение вида |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x¢2 × |
|
2 |
× |
|
|
2 |
- y¢2 |
× |
2 |
× |
|
2 |
= m |
или |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|||||
|
x′2 |
|
- |
y′2 |
|
=1 – это уравнение гиперболы с полуосями a = b = |
|
. |
|||||||||||||
|
|
2m |
|||||||||||||||||||
|
2m |
2m |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y′ |
y |
|
x′ |
||
|

 2m
2m

 2m
2m
x
- 
 2m
2m
- 
 2m
2m
Рис. 16.
Замечание. С помощью поворота координатных осей удается избавиться от слагаемого, содержащего произведение xy .
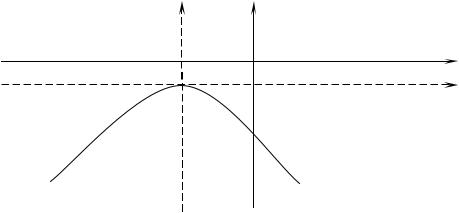
Пример. 3. Привести к простейшему виду и построить кривую, за-
данную уравнением: |
x2 |
+ 4x + 3y + 6 = 0 . |
|
|
|
|||
Решение. AC − B2 |
= 0 – кривая параболического типа. Сгруппируем |
|||||||
полный квадрат и преобразуем данное уравнение: |
|
|||||||
x2 + 4x + 4 − 4 + 3y + 6 = 0 |
|
|
|
|||||
2 |
|
|
2 |
|
x + 2 |
= x¢ |
|
|
|
|
|
|
|
||||
(x + 2) |
= -3 y |
+ |
|
|
.Положим, что |
2 |
= y¢ |
являются формулами |
|
||||||||
|
|
|
3 |
|
y + |
|
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
параллельного переноса в т.O1 |
|
- 2,- |
2 |
|
. Получим уравнение: |
x′2 = -3y′ – |
|||||
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
|
||
парабола с вершиной в т. O1 |
|
- 2,- |
2 |
|
|
|
|
|
|||
|
|
|
|
и симметричная относительно оси |
|||||||
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
|
||
oy′. |
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
|
|
y |
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
O |
|
|||
|
O1 |
|
|
|
|
|
− |
2 |
|
x′ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
3 |
|
||
|
|
|
|
-2 |
|
|
|
|
|||
Рис. 17.
|
|
Пример 4. Построить кривую y = |
|
x + 3 |
. |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x +1 |
||
|
|
Решение. Перепишем уравнение 2xy - x + y - 3 = 0 , 2x + 1 ¹ 0 . |
|||||||||||||||||||||||
AC − B2 = −4 < 0 – |
кривая гиперболического типа. |
||||||||||||||||||||||||
|
|
Преобразуем данное уравнение: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
5 |
|
|
|
|
|
|||||||
|
|
2 y x + |
|
|
− |
x |
+ |
|
− |
|
= 0 |
|
|
|
|
||||||||||
|
2 |
2 |
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
||||
|
|
x + |
|
y − |
|
|
= |
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
4 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x + |
1 |
|
= x′ |
|
|
|
|
|
5 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Положим |
|
|
|
2 |
|
|
|
|
. Получим x¢ × y¢ = |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
y − |
1 |
= y′ |
|
|
|
|
4 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
O¢ |
- |
1 |
, |
1 |
|
– |
|
новое начало координат после параллельного переноса. |
|||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
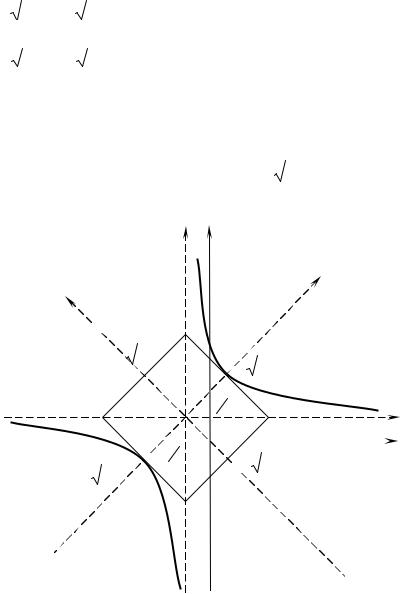
Повернем оси координат o′x′ и o′y′ на угол 45o |
(см. пример 2). |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x′ = x′′ |
|
|
|
− y′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = x′′ |
2 |
|
|
− y′′ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получим уравнение (x¢¢)2 × |
1 |
- (y¢¢)2 × |
1 |
= |
5 |
, |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
(x′′)2 |
− (y′′)2 |
|
|
|
2 |
|
2 |
4 |
|
|
|
|
|
|||||||||||||||||
=1 – |
|
|
|
|
|
|
a = b = |
|
. |
|
||||||||||||||||||||
|
гипербола, где |
2,5 |
|
|||||||||||||||||||||||||||
2,5 |
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
y |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
y′′ |
|
|
|
|
|
|
|
|
|
|
x′′ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O′ |
12 |
|
|
|
|
|
|
|
|
|
|
x′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
− |
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
− |
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 18.
Задание 1
1.01. Составить уравнение эллипса, имеющего общие фокусы с ги-
перболой x2 − 2 y 2 |
= 24 , если эксцентриситет равен |
3 |
. |
|
|
|
|
|
||
5 |
|
|
|
|
|
|||||
1.02. Найти |
|
|
|
|
|
|
|
|
|
|
расстояние |
от |
центра |
|
|
окружности |
|||||
x2 + y 2 + 6x + 2 y − 5 = 0 до асимптот гиперболы 9x2 |
−16 y 2 |
=144 . |
||||||||
1.03. На параболе y 2 = 32x взяты две точки |
M |
1 |
и |
M |
2 |
, расстояния |
||||
|
|
|
|
|
|
|
|
|
||
которых до фокуса этой параболы равны 10. Составить уравнение окружности, диаметром которой является отрезок M1 M 2 .
1.04. Вершины эллипса, большая ось которого лежит на оси абсцисс, совпадают с вершинами равносторонней гиперболы. Составить уравнения
обеих кривых, если известно, что точка M (6, 2), лежащая на гиперболе, равноудалена от ближайших к ней фокусов эллипса и гиперболы.
1.05. Ось симметрии параболы параллельна оси ординат, а уравнение директрисы y −10 = 0 . Составить уравнение параболы, если она пересекает ось ox в точках (− 5,0) и (11,0).
1.06. Вершина параболы совпадает с одним из фокусов гиперболы 9x2 −16 y 2 =144 . Составить уравнение параболы, если известно, что ее директриса проходит через точки (− 4,−3) и (− 4,3).
1.07. Директриса параболы пересекает эллипс 9x2 + 20 y 2 = 324 в точках (− 4,3) и (4,3), а расстояние от этих точек до фокуса параболы рав-
но 2
 5 . Составить уравнение параболы.
5 . Составить уравнение параболы.
1.08. Равносторонняя гипербола x2 − y 2 =16 проходит через фокусы эллипса. Составить простейшее уравнение этого эллипса, если отношение
эксцентриситетов гиперболы и эллипса равно |
3 . |
|
|
|||
1.09. Найти |
длину |
стороны |
квадрата, |
вписанного |
в эллипс |
|
9x2 +16 y 2 = 576 . |
|
|
|
|
|
|
1.10. Найти |
угол, |
под |
которым |
из фокуса |
параболы |
|
x2 − 4x + 8 y − 20 = 0 видна большая ось эллипса x2 |
+ 2 y 2 =16 . |
|
||||
1.11.Написать каноническое уравнение эллипса, если его большая ось равна 16 , а фокусы отстоят от вершин на 0, 2 от ее длины.
1.12.Меридиан земного шара имеет форму эллипса, отношение осей
которого равно 299 . Определить эксцентриситет земного меридиана.
|
|
300 |
1.13. Написать уравнение окружности, проходящей через точки |
||
(−1, 2) и (3,0), зная, что ее центр лежит на прямой x − y + 2 = 0 . |
||
1.14. Написать уравнение гиперболы, имеющей общие фокусы с эл- |
||
липсом x2 |
+ y 2 |
=1, если ее эксцентриситет равен 1, 25. |
4924
1.15.На эллипсе x2 + y 2 =1 найти точку, отстоящую на расстояние
30 24
пяти единиц от его малой оси.
1.16.Прямые x = 8, x = −8 служат директрисами эллипса, малая ось которого равна 8 . Найти уравнение этого эллипса.
1.17.Эллипс проходит через точки M (
 3,−2) и N (− 2
3,−2) и N (− 2
 3,1). Соста-
3,1). Соста-
вить уравнение эллипса, приняв его оси за оси координат.
1.18. Составить уравнение гиперболы, |
проходящей через точку |
||
A(9,−8), если асимптоты ее заданы уравнениями |
|
|
x ± 3y = 0 . |
|
2 |
||
1.19. Написать каноническое уравнение параболы с вершиной в начале координат, если известно, что ее фокус находится в точке пересечения прямой 4x − 3y − 4 = 0 с осью ox .
